[Mathmatics for ML] 2. Convex Optimization

• KKT condition이 무엇인지, Lagrange function과 어떤 관련이 있는지

Optimization : 최적화

gradient descent : 경사 하강법

infimum : 하한

convex : 볼록

concave : 오목

 

Optimization의 목표 : n개의 training data에 대한 model의 parameter 최적화 ($minL(\theta)$)

---

• 각 iteration에서 사용하는 데이터의 양에 따른 분류
  1. Batch gradient descent
  2. Mini-batch gradient descent
  3. Stochastic gradient descent
• 적응형 업데이트 방법에 따른 분류
  • Momentum, NAG, Adagrad, RMSprop, Adam,,,

---

1. Optimization Using Gradient Descent

[Unconstrained Optimization]

$\mathbf{x}_{k+1} = \mathbf{x}_k + \gamma_k \mathbf{d}_k$

Steepest Gradient descent : $\mathbf{d}_k = -\nabla f(\mathbf{x}_k)^\top$

⇒ 다음 스텝 값이 내려가도록

$X_{k+1}$ 구하는 예시

$L(\theta) = \sum_{i=1}^{n} L_n(\theta)$ 라고 가정할 때

$\theta_{k+1} = \theta_k - \gamma_k \nabla L(\theta_k)^\top = \theta_k - \gamma_k \sum_{n=1}^{N} \nabla L_n(\theta_k)^\top$

⇒ n이 클수록 업데이트마다의 계산량이 큼

Batch gradient

• $\sum_{n=1}^{N} \nabla L_n(\theta_k)^\top$
• 매 번 모든 loss의 sum만큼 계산, 업데이트 실행

Mini-batch gradient

• $\sum_{n \in \mathcal{K}} \nabla L_n(\theta_k)^\top$, $|\mathcal{K}| < n$
• 일부의 loss의 sum만큼 계산, 업데이트 실행
• Stochastic gradient에 속함

Stochastic Gradient Descent (SGD)

• $\sum_{n=1}^{N} \nabla L_n(\theta_k)^\top = E\left[ \sum_{n \in \mathcal{K}} \nabla L_n(\theta_k)^\top \right]$
• original full batch = subset을 구한 gradient의 expectation

Momentum

• 이전의 방향을 어느정도 유지하며 업데이트하자!

$\mathbf{x}_{k+1} = \mathbf{x}_k - \gamma_k \nabla f(\mathbf{x}_k)^\top + \alpha \Delta \mathbf{x}_k, \quad \alpha \in [0,1]$

$\Delta \mathbf{x}_k = \mathbf{x}k - \mathbf{x}{k-1}$ : 이전에 업데이트 했던 방향

$\alpha$ : 얼마나 이전의 값을 가져갈건지

2. Constrained Optimization and Lagrange Multipliers

Lagrange Multipliers를 활용해 Constrained Optimization을 unconstrained optimization처럼 쉽게 풀 수 있게 만들기

• $p^*$ : Optimal value
• $x^*$ : Optimizer

< 조건 >

$g_i(\mathbf{x}) \leq 0, \quad i = 1, 2, \ldots, m \quad \text{(Inequality constraints)}$

$h_j(\mathbf{x}) = 0, \quad j = 1, 2, \ldots, p \quad \text{(Equality constraints)}$

 

Lagrangian : $\mathcal{L}(\mathbf{x}, \boldsymbol{\lambda}, \boldsymbol{\nu}) = f(\mathbf{x}) + \sum_{i=1}^{m} \lambda_i g_i(\mathbf{x}) + \sum_{i=1}^{p} \nu_i h_i(\mathbf{x})$

Lagrange multipliers : ${\lambda} = (\lambda_i : i = 1, \ldots, m) \succeq 0, \quad \boldsymbol{\nu} = (\nu_1, \ldots, \nu_p)$

Lagrange dual function : $\mathcal{D}({\lambda}, {\nu}) = \inf_{\mathbf{x}} \mathcal{L}(\mathbf{x}, {\lambda}, {\nu})$

• $\lambda, \nu$를 고정했을 때 x에 대한 infimum
• 풀면 best lower bound를 찾을 수 있음

$\mathcal{L}(\tilde{\mathbf{x}}, \boldsymbol{\lambda}, \boldsymbol{\nu}) = f(\tilde{\mathbf{x}}) + \sum_{i=1}^{m} \lambda_i g_i(\tilde{\mathbf{x}}) + \sum_{i=1}^{p} \nu_i h_i(\tilde{\mathbf{x}}) \leq f(\tilde{\mathbf{x}})$

$\lambda_i >= 0, g_i(\tilde{\mathbf{x}}) <= 0, h_j(x) =0$

$\mathcal{D}(\boldsymbol{\lambda}, \boldsymbol{\nu}) \leq \mathcal{L}(\tilde{\mathbf{x}}, \boldsymbol{\lambda}, \boldsymbol{\nu}) \leq f(\tilde{\mathbf{x}})$

D(λ,ν)가 λ,ν에 대해 concave 함수라 (λ,ν)는 항상 convex optimization

 

$d^*≤ p^*$

• $d^*$ : dual optimization
• $p^*$ : primal optimization
• $p^* - d^*$ : Optimal duality gap

3. Convex Sets and Functions

• $\mathbf{x} \in \mathcal{X}, f(\mathbf{x}) : \mathbb{R}^n \to \mathbb{R}$ 이 convex function이라면 $\mathcal{X}$ : convex set

Convex Set

• x1,x2 선분이 set 안에 포함되어있을 때 : convex set

• 선분의 일부가 set 안에 포함되어있지 않을 때 convex set이 아님

convex function

$f(\theta \mathbf{x} + (1 - \theta) \mathbf{y}) \leq \theta f(\mathbf{x}) + (1 - \theta) f(\mathbf{y})$

• -$f$가 convex function이면 $f$는 concave function

convex function의 조건

1. 함수가 미분가능할 때, 접선보다 항상 함수가 위에 있다면 ( $f(\mathbf{y}) - f(\mathbf{x}) \geq \nabla f(\mathbf{x})^\top (\mathbf{y} - \mathbf{x})$)
   1-1. $\nabla f(\mathbf{x}) = 0$, $f(y)$≥$f(x)$라면, $x$는 $f$의 global minima
   1-2. function의 global optima = $\nabla f(\mathbf{x}) = 0$ (local optima)
2. $f$가 convex function이라면, $\nabla^2 f(\mathbf{x}) \succeq 0$

convex function의 속성

1. $g(x) = f(Ax+b)$가 convex func이라면 $f(x)$도 convex function
2. $f_1(x), f_2(x)\text{가 convex func이라면, }f(x) = max(f_1(x), f_2(x))도 \text{ convex func}$
3. $f(x,y)$가 convex, y가 고정일 때, $g(\mathbf{x}) = \sup_{y \in A} f(\mathbf{x}, y)$ ($g(x)$의 상한도 convex)
   3-1. $f(x,y)$가 concave일 때, $g(\mathbf{x}) = \inf_{y \in A} f(\mathbf{x}, y) \text{ (g(x)의 하한도 concave)}$

4. Convex Optimization

Convex function을 convex set이 주어지고 하는 optimization

• Convex Optimization : $d^* = p^*$
• convexity function + 제약조건이 있다면 ⇒ strong duality ( $d^* = p^*$)

ex)

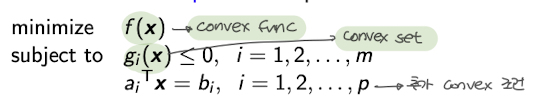
KKT Condition : 대표적인 convex optimization의 수학적 특징

$x∗\text{가 x에 대해 }L(x,λ∗,ν∗)\text{ 을 최소화함}$

⇒ $\nabla f(\mathbf{x}^) + \sum_{i=1}^{m} \lambda_i^ \nabla g_i(\mathbf{x}^) + \sum_{i=1}^{p} \nu_i^ \nabla h_i(\mathbf{x}^*) = 0$

Karush-Kuhn-Tucker optimality condition $(x^, \lambda^\text{이 해당 조건 만족 시 KKT condition 만족})$

$g_i(\mathbf{x}^) \leq 0, \quad h_i(\mathbf{x}^) = 0, \quad \lambda_i^* \succeq 0$ $\lambda_i^* g_i(\mathbf{x}^) = 0$ $\nabla f(\mathbf{x}^) + \sum_{i=1}^{m} \lambda_i^* \nabla g_i(\mathbf{x}^) + \sum_{i=1}^{p} \nu_i^ \nabla h_i(\mathbf{x}^*) = 0$ x에 대한 gradient에 대해 lagrangian func의 gradient가 0이 되어야 하는 조건